MAXimal :: algo :: Метод Гаусса рішення системи лінійних рівнянь

1. алгоритм Гауса
2. Базова схема
3. Пошук опорного елемента (pivoting)
4. вироджені випадки
5. Реалізація
6. асимптотика
7. Більш точна оцінка числа дій
8. додатки
9. Рішення СЛАР за модулем
10. Трохи про різні способи вибору опорного елемента
11. Поліпшення знайденого відповіді

додано: 11 Jun 2008 11:11
Змінено: 2 May 2012 0:40

дана система 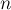лінійних алгебраїчних рівнянь (СЛАР) з невідомими. Потрібно вирішити цю систему: визначити, скільки рішень вона має (ні одного, одне або нескінченно багато), а якщо вона має хоча б одне рішення, то знайти будь-яке з них.

Формально задача ставиться таким чином: вирішити систему:

де коефіцієнти і 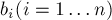відомі, а змінні - шукані невідомі.

Зручно матричне подання цього завдання:

де 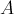- матриця 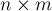, Складена з коефіцієнтів 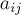, і - вектори-стовпці висоти .

Варто відзначити, що СЛАР може бути не над полем дійсних чисел, а над полем по модулю будь-якого числа , Тобто .:

- алгоритм Гаусса працює і для таких систем теж (але цей випадок буде розглянутий нижче в окремому розділі).

алгоритм Гауса

Строго кажучи, описуваний нижче метод правильно називати методом "Гаусса-Жордана" (Gauss-Jordan elimination), оскільки він є варіацією методу Гаусса, описаної геодезистом Вільгельмом Жорданом в 1887 р (варто зазначити, що Вільгельм Жордан не є автором ні теореми Жордана про кривих, ні жорданової алгебри - все це три різних вчених-однофамільця, крім того, по всій видимості, більш правильною є транскрипція "Йордан", але написання "Жордан" вже закріпилася в російській літературі). Також цікаво зауважити, що одночасно з Жорданом (а за деякими даними навіть раніше за нього) цей алгоритм придумав Класен (B.-I. Clasen).

Базова схема

Коротко кажучи, алгоритм полягає в послідовному виключенні змінних з кожного рівняння до тих пір, поки в кожному рівнянні не залишиться тільки по одній змінній. якщо 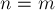, То можна говорити, що алгоритм Гаусса-Жордана прагне привести матрицю 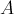системи до одиничної матриці - адже після того як матриця стала одиничною, рішення системи очевидно - рішення єдино і задається отриманими коефіцієнтами .

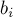При цьому алгоритм грунтується на двох простих еквівалентних перетвореннях системи: по-перше, можна обмінювати два рівняння, а по-друге, будь-яке рівняння можна замінити лінійною комбінацією цього рядка (з ненульовим коефіцієнтом) і інших рядків (з довільними коефіцієнтами).

На першому кроці алгоритм Гаусса-Жордана ділить перший рядок на коефіцієнт 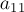. Потім алгоритм додає перший рядок до інших рядках з такими коефіцієнтами, щоб їх коефіцієнти в першому стовпці зверталися в нулі - для цього, очевидно, при додаванні першого рядка до -ої треба домножать її на . При кожній операції з матрицею 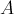(Розподіл на число, поповнення лише до рядку інший) відповідні операції проводяться і з вектором ; в певному сенсі, він поводиться, як якщо б він був 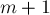-им стовпчиком матриці .

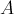У підсумку, після закінчення першого кроку перший стовпець матриці 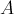стане одиничним (тобто міститиме одиницю в першому рядку і нулі в інших).

Аналогічно проводиться другий крок алгоритму, тільки тепер розглядається другий стовпець і другий рядок: спочатку другий рядок ділиться на 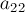, А потім віднімається від всіх інших рядків з такими коефіцієнтами, щоб обнуляти другий стовпець матриці .

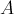І так далі, поки ми не опрацюємо всі рядки або всі стовпці матриці 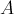. якщо 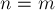, То з побудови алгоритму очевидно, що матриця 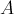вийде одиничної, що нам і потрібно.

Пошук опорного елемента (pivoting)

Зрозуміло, описана вище схема неповна. Вона працює тільки в тому випадку, якщо на кожному -ом кроці елемент відмінний від нуля - інакше ми просто не зможемо домогтися обнулення інших коефіцієнтів в поточному стовпці шляхом додавання до них -ої рядки.

Щоб зробити алгоритм працює в таких випадках, як раз і існує процес вибору опорного елемента (на англійській мові це називається одним словом "pivoting"). Він полягає в тому, що виробляється перестановка рядків і / або стовпців матриці, щоб в потрібному елементі виявилося нульове число.

Зауважимо, що перестановка рядків значно простіше реалізується на комп'ютері, ніж перестановка стовпців: адже при обміні місцями двох якихось стовпців треба запам'ятати, що ці дві змінних обмінялися місцями, щоб потім, при відновленні відповіді, правильно відновити, яку відповідь до якої змінної ставиться . При перестановці рядків ніяких таких додаткових дій робити не треба.

На щастя, для коректності методу досить одних тільки обмінів рядків (т.зв. "partial pivoting", на відміну від "full pivoting", коли обмінюються і рядки, і стовпці). Але яку ж саме рядок слід вибирати для обміну? І чи правда, що пошук опорного елемента треба робити тільки тоді, коли поточний елемент нульовий?

Загальної відповіді на це питання не існує. Є різноманітні евристики, проте найефективнішою з них (по співвідношенню простоти і віддачі) є така евристика: як опорний елемент слід брати найбільший по модулю елемент, причому проводити пошук опорного елемента і обмін з ним треба завжди, а не тільки коли це необхідно ( тобто не тільки тоді, коли ).

Іншими словами, перед виконанням -ої фази алгоритму Гаусса-Жордана з евристикою partial pivoting необхідно знайти в -ом стовпці серед елементів з індексами від до 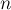максимальний по модулю, і обміняти рядок з цим елементом з -ої рядком.

По-перше, ця евристика дозволить вирішити СЛАР, навіть якщо по ходу рішення буде траплятися так, що елемент . По-друге, що дуже важливо, ця евристика покращує чисельну стійкість алгоритму Гаусса-Жордана.

Без цієї евристики, навіть якщо система така, що на кожній -ої фазі - алгоритм Гаусса-Жордана відпрацює, але в підсумку накопичується похибка може виявитися настільки величезною, що навіть для матриць розміру близько 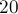похибка буде перевершувати сам відповідь.

вироджені випадки

Отже, якщо зупинятися на алгоритмі Гаусса-Жордана з partial pivoting, то, стверджується, якщо 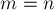і система невирождени (тобто має ненульовий визначник, що означає, що вона має єдине рішення), то описаний вище алгоритм повністю відпрацює і прийде до одиничної матриці 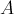(Доказ цього, тобто того, що ненульовий опорний елемент завжди буде знаходитися, тут не наводиться).

Розглянемо тепер загальний випадок - коли 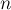і не обов'язково рівні. Припустимо, що опорний елемент на -ом кроці не знайшов. Це означає, що в -ом стовпці всі рядки, починаючи з поточної, містять нулі. Стверджується, що в цьому випадку ця -а змінна не може бути визначена, і є незалежною змінною (може приймати довільне значення). Щоб алгоритм Гаусса-Жордана продовжив свою роботу для всіх наступних змінних, в такій ситуації треба просто пропустити поточний -ий стовпець, не збільшуючи при цьому номер поточного рядка (можна сказати, що ми віртуально видаляємо -ий стовпець матриці).

Отже, деякі змінні в процесі роботи алгоритму можуть надаватися незалежними. Зрозуміло, що коли кількість змінних більше кількості 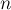рівнянь, то як мінімум 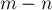змінних виявляться незалежними.

В цілому, якщо виявилася хоча б одна незалежна змінна, то вона може приймати довільне значення, в той час як інші (залежні) змінні будуть виражатися через неї. Це означає, що, коли ми працюємо в поле дійсних чисел, система потенційно має нескінченно багато рішень (якщо ми розглядаємо СЛАР по модулю, то число рішень дорівнюватиме цього модулю в ступеня кількості незалежних змінних). Втім, слід бути акуратним: треба пам'ятати про те, що навіть якщо були виявлені незалежні змінні, проте СЛАР може не мати рішень зовсім. Це відбувається, коли в останніх необробленими рівняннях (тих, до яких алгоритм Гаусса-Жордана не дійшов, тобто це рівняння, в яких залишилися тільки незалежні змінні) є хоча б один ненульовий вільний член.

Втім, простіше це перевірити явною підстановкою знайденого рішення: всім незалежними змінним привласнити нульові значення, залежним змінним привласнити знайдені значення, і підставити це рішення в поточну СЛАР.

Реалізація

Наведемо тут реалізацію алгоритму Гаусса-Жордана з евристикою partial pivoting (вибором опорного елемента як максимуму за стовпцем).

На вхід функції 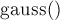передається сама матриця системи . Останній стовпець матриці - це в наших старих позначеннях стовпець вільних коефіцієнтів (так зроблено для зручності програмування - тому що в самому алгоритмі всі операції з вільними коефіцієнтами повторюють операції з матрицею ).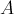

Функція повертає число рішень системи ( 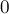, або ) (Нескінченність позначена в коді спеціальної константою , Якій можна задати будь-яке велике значення). Якщо хоча б одне рішення існує, то воно повертається в векторі .

int gauss (vector <vector <double>> a, vector <double> & ans) {int n = (int) a. size (); int m = (int) a [0]. size () - 1; vector <int> where (m, - 1); for (int col = 0, row = 0; col <m && row <n; ++ col) {int sel = row; for (int i = row; i <n; ++ i) if (abs (a [i] [col])> abs (a [sel] [col])) sel = i; if (abs (a [sel] [col]) <EPS) continue; for (int i = col; i <= m; ++ i) swap (a [sel] [i], a [row] [i]); where [col] = row; for (int i = 0; i <n; ++ i) if (i! = row) {double c = a [i] [col] / a [row] [col]; for (int j = col; j <= m; ++ j) a [i] [j] - = a [row] [j] * c; } ++ row; } Ans. assign (m, 0); for (int i = 0; i <m; ++ i) if (where [i]! = - 1) ans [i] = a [where [i]] [m] / a [where [i]] [ i]; for (int i = 0; i <n; ++ i) {double sum = 0; for (int j = 0; j <m; ++ j) sum + = ans [j] * a [i] [j]; if (abs (sum - a [i] [m])> EPS) return 0; } For (int i = 0; i <m; ++ i) if (where [i] == - 1) return INF; return 1; }

У функції підтримуються два покажчика - на поточний стовпець 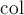і поточний рядок .

Також заводиться вектор 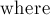, В якому для кожної змінної записано, в якому рядку повинна вона вийти (іншими словами, для кожного стовпця записаний номер рядка, в якій цей стовпець відмінний від нуля). Цей вектор потрібен, оскільки деякі змінні могли не "визначитися" в ході рішення (тобто це незалежні змінні, яким можна привласнити довільне значення - наприклад, в наведеній реалізації це нулі).

Реалізація використовує техніку partial pivoting, виробляючи пошук рядка з максимальним по модулю елементом, і переставляючи потім цей рядок в позицію (Хоча явну перестановку рядків можна замінити обміном двох індексів в деякому масиві, на практиці це не дасть реального виграшу, тому що на обміни витрачається операцій).

У реалізації з метою простоти поточний рядок не ділиться на опорний елемент - так що в підсумку після закінчення роботи алгоритму матриця стає одиничною, а діагональної (втім, мабуть, поділ рядка на провідний елемент дозволяє дещо зменшити виникають похибки).

Після знаходження рішення воно підставляється назад в матрицю - щоб перевірити, чи має система хоча б одне рішення чи ні. Якщо перевірка знайденого рішення пройшла успішно, то функція повертає або - в залежності від того, чи є хоча б одна незалежна змінна чи ні.

асимптотика

Оцінимо асимптотику отриманого алгоритму. Алгоритм складається з фаз, на кожній з яких відбувається:

Очевидно, перший пункт має меншу асимптотику, ніж другий. Зауважимо також, що другий пункт виконується не більше раз - стільки, скільки може бути залежних змінних в СЛАР.

Таким чином, підсумкова асимптотика алгоритму набирає вигляду .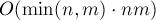

при ця оцінка перетворюється в .

Зауважимо, що коли СЛАР розглядається не в полі дійсних чисел, а в поле по модулю два, то систему можна вирішувати набагато швидше - про це див. Нижче в розділі "Рішення СЛАР за модулем".

Більш точна оцінка числа дій

Для простоти викладок вважатимемо, що .

Як ми вже знаємо, час роботи всього алгоритму фактично визначається часом, що витрачається на виключення поточного рівняння з інших.

Це може відбуватися на кожному з 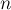кроків, при цьому поточний рівняння додається до всіх іншим. При додаванні робота йде тільки за допомогою стовпців, починаючи з поточного. Таким чином, в сумі виходить операцій.

додатки

Прискорення алгоритму: поділ його на прямий і зворотний хід

Досягти дворазового прискорення алгоритму можна, розглянувши іншу його версію, більш класичну, коли алгоритм розбивається на фази прямого і зворотного ходу.

В цілому, на відміну від описаного вище алгоритму, можна приводити матрицю ні до діагонального вигляду, а до трикутного вигляду - коли всі елементи строго нижче головної діагоналі дорівнюють нулю.

Система з трикутною матрицею вирішується тривіально - спочатку з останнього рівняння відразу знаходиться значення останньої змінної, потім знайдене значення підставляється в передостаннє рівняння і знаходиться значення передостанній змінної, і так далі. Цей процес і називається зворотним ходом алгоритму Гаусса.

Прямий хід алгоритму Гаусса - це алгоритм, аналогічний описаному вище алгоритму Гаусса-Жордана, за одним винятком: поточна змінна виключається не з усіх рівнянь, а тільки з рівнянь після поточного. В результаті цього дійсно виходить не діагональна, а трикутна матриця.

Різниця в тому, що прямий хід працює швидше алгоритму Гаусса-Жордана - оскільки в середньому він робить в два рази менше додатків одного рівняння до іншого. Зворотний хід працює за , Що в будь-якому випадку асимптотично швидше прямого ходу.

Таким чином, якщо 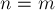, То даний алгоритм буде робити вже 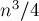операцій - що в два рази менше алгоритму Гаусса-Жордана.

Рішення СЛАР за модулем

Для вирішення СЛАР по модулю можна застосовувати описаний вище алгоритм, він зберігає свою коректність.

Зрозуміло, тепер стає непотрібним використовувати якісь хитрі техніки вибору опорного елемента - досить знайти будь-який ненульовий елемент в поточному стовпці.

Якщо модуль простий, то ніяких складнощів взагалі не виникає - що відбуваються по ходу роботи алгоритму Гаусса розподілу не створюють особливих проблем.

Особливо чудовий модуль, що дорівнює двом: для нього всі операції з матрицею можна виробляти дуже ефективно. Наприклад, віднімання одного рядка від іншої по модулю два - це насправді їх симетрична різниця ( "xor"). Таким чином, весь алгоритм можна значно прискорити, стиснувши всю матрицю в бітові маски і оперуючи тільки ними. Наведемо тут нову реалізацію основної частини алгоритму Гаусса-Жордана, використовуючи стандартний контейнер C ++ "bitset":

int gauss (vector <bitset <N>> a, int n, int m, bitset <N> & ans) {vector <int> where (m, - 1); for (int col = 0, row = 0; col <m && row <n; ++ col) {for (int i = row; i <n; ++ i) if (a [i] [col]) { swap (a [i], a [row]); break; } If (! A [row] [col]) continue; where [col] = row; for (int i = 0; i <n; ++ i) if (i! = row && a [i] [col]) a [i] ^ = a [row]; ++ row; }

Як можна помітити, реалізація стала навіть трохи коротше, при тому, що вона значно швидше старої реалізації - а саме, швидше в 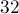рази за рахунок бітового стиснення. Також слід зазначити, що рішення систем по модулю два на практиці працює дуже швидко, оскільки випадки, коли від одного рядка треба забирати іншу, відбуваються досить рідко (на розріджених матрицях цей алгоритм може працювати за час швидше порядку квадрата від розміру, ніж куба).

Якщо модуль довільний (не обов'язково простий), то все стає трохи складніше. Зрозуміло, що користуючись Китайської теоремою про залишки , Ми зводимо задачу з довільним модулем тільки до модулів виду "ступінь простого". [Подальший текст був прихований, тому що це неперевірена інформація - можливо, неправильний спосіб вирішення]

Нарешті, розглянемо питання числа рішень СЛАР по модулю. Відповідь на нього досить простий: число рішень одно 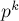, де - модуль, 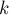- число незалежних змінних.

Трохи про різні способи вибору опорного елемента

Як вже говорилося вище, однозначної відповіді на це питання немає.

Евристика "partial pivoting", яка полягала в пошуку максимального елемента в поточному стовпці, працює на практиці досить непогано. Також виявляється, що вона дає практично той же результат, що і "full pivoting" - коли опорний елемент шукається серед елементів цілої подматріци - починаючи з поточного рядка і з поточного стовпчика.

Але цікаво відзначити, що обидві ці евристики з пошуком максимального елемента, фактично, дуже залежать від того, наскільки були промасштабіровани вихідні рівняння. Наприклад, якщо одне з рівнянь системи помножити на мільйон, то це рівняння майже напевно буде вибрано в якості ведучого на першому ж кроці. Це здається досить дивним, тому логічний перехід до трохи більш складною евристиці - так званому "implicit pivoting".

Евристика implicit pivoting полягає в тому, що елементи різних рядків порівнюються так, як якщо б обидві рядки були пронормовані таким чином, що максимальний по модулю елемент в них був би дорівнює одиниці. Для реалізації цієї техніки треба просто підтримувати поточний максимум в кожному рядку (або підтримувати кожен рядок так, щоб максимум в ній дорівнював одиниці по модулю, але це може привести до збільшення накопичуваної похибки).

Поліпшення знайденого відповіді

Оскільки, незважаючи на різні евристики, алгоритм Гаусса-Жордана все одно може призводити до великих погрішностей на спеціальних матрицях навіть розмірів порядку - .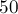

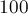У зв'язку з цим, отриманий алгоритмом Гауса-Жордана відповідь можна поліпшити, застосувавши до нього будь-якої простої чисельний метод - наприклад, метод простої ітерації.

Таким чином, рішення перетворюється в двокрокового: спочатку виконується алгоритм Гаусса-Жордана, потім - будь-якої чисельний метод, який приймає в якості початкових даних рішення, отримане на першому кроці.

Такий прийом дозволяє дещо розширити безліч завдань, що вирішуються алгоритмом Гауса-Жордана з прийнятною похибкою.

література